Yılan ve Merdiven Problemi

Yılan ve merdiven problemini çoğu kişi oyun olarak biliyor. Yılan ve merdiven problemi ile ilgili kısa bir bilgi verelim. Bu oyunun çok ilgi çekici bir oyun alanı, levhası var. Balinadan tavus kuşuna kadar çeşitli hayvanlar kareleri süslüyor. Bu arada tabii yılanlarla, merdivenler hemen el altında bulunuyor. Oyun tek veya iki zarla oynanıyor. Oyuna başlamak için oyunculardan birinin 6 atması gerekiyor. Ondan sonraki hamleler zarda görülen rakam gereğince oyun alanının aşağısından başlamak üzere başlıyor. 6 atan veya buna eşdeğer çift atan (5-5 gibi) oyuncu yılanı ve merdiveni ile zarın gösterdiği rakam kadar yukarıya doğru tırmanıyor.

Batı dünyasındaki küçüklerin ilgisini çeken merdiven, yılan oyununda ana amaç 100 rakamına, yani en tepeye ulaşmak. Örneğin 99’daki bir oyuncu eğer 2 atarsa bu takdirde 101 rakamına elde ediyor. İşte bu anda bir kare geri gitmesi gerekiyor. Çünkü oyunda karelerde gösterilen rakamlarından ne bir eksik, ne bir fazla rakam atmak işe yaramıyor. Çünkü bunun cezası bir kare geriye gitmek oluyor. Kısacası gereksinmesi ne kadarsa oyuncunun o kadar sayı atması şart oluyor. Oyunda merdivenlerin ve yılan kafalarının zarda atılan sayı kadar sağa ve sola gideceğini söylemenin gereği yok. Çünkü bu kendiliğinden anlaşılıyor. Yılan ve merdiven problemi için pek çok varyasyon mevcuttur.

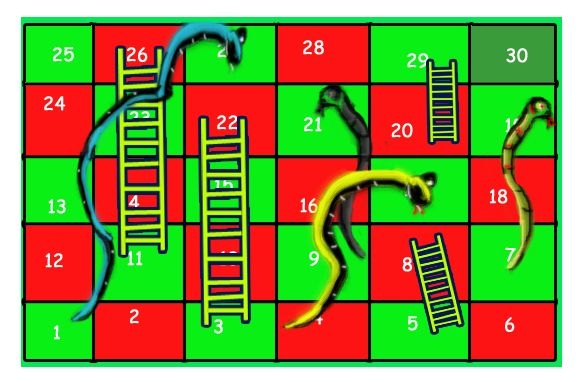
Örneğin, gösterilen tahtayı düşünün, 1.hücreden 30. hücreye ulaşmak için gereken minimum zar sayısı 3’tür.

Adımları takip edin:

• Önce 3 numaralı hücreye ulaşmak için iki zar atın ve sonra 22’ye ulaşmak için merdiveni kullanın.
• Sonra 28’e ulaşmak için 6’yı atın.
• Sonunda 2 ile 30’a ulaşabilirsiniz.

(2, 2, 6), (2, 4, 4), (2, 3, 5) gibi başka çözümler de olabilir.

Buradaki fikir, verilen yılan ve merdiven tahtasını, tahtadaki hücre sayısına eşit köşe sayısına sahip yönlendirilmiş bir grafik olarak düşünmektir. Sorun, bir grafikte en kısa yolu bulmaya indirgenir. Bir sonraki 6 köşenin bir yılan veya merdiveni yoksa, grafiğin her köşesinin bir sonraki altı köşesine bir kenarı vardır. Sonraki altı köşeden herhangi birinin bir yılan veya merdiveni varsa, o zaman mevcut köşeden gelen kenar, yılanın merdiveninin veya kuyruğunun tepesine gider.

Problem için en az 3 zar atılmalıdır.

Yukarıdaki çözümün zaman karmaşıklığı O(N)’dir, çünkü her hücre kuyruktan yalnızca bir kez eklenir ve kaldırılır. Ve tipik bir enqueue veya dequeue işlemi O(1) zaman alır.

JAVA

Bu problemin çözümünü Java kullanarak sizlere anlatmak istedik.

// Java program to find minimum number of dice 
// throws required to reach last cell from first 
// cell of a given snake and ladder board 
import java.util.LinkedList; 
import java.util.Queue; 
public class SnakesLadder 
{ 
// An entry in queue used in BFS 
static class qentry 
{ 
int v;// Vertex number 
int dist;// Distance of this vertex from source 
} 
// This function returns minimum number of dice 
// throws required to Reach last cell from 0'th cell 
// in a snake and ladder game. move[] is an array of 
// size N where N is no. of cells on board If there 
// is no snake or ladder from cell i, then move[i] 
// is -1 Otherwise move[i] contains cell to which 
// snake or ladder at i takes to. 
static int getMinDiceThrows(int move[], int n) 
{ 
int visited[] = new int[n]; 
Queue<qentry> q = new LinkedList<>(); 
qentry qe = new qentry(); 
qe.v = 0; 
qe.dist = 0; 
// Mark the node 0 as visited and enqueue it. 
visited[0] = 1; 
q.add(qe); 
// Do a BFS starting from vertex at index 0 
while (!q.isEmpty()) 
{ 
qe = q.remove(); 
int v = qe.v; 
// If front vertex is the destination 
// vertex, we are done 
if (v == n - 1) 
break; 
// Otherwise dequeue the front vertex and 
// enqueue its adjacent vertices (or cell 
// numbers reachable through a dice throw) 
for (int j = v + 1; j <= (v + 6) && j < n; ++j) 
{ 
// If this cell is already visited, then ignore 
if (visited[j] == 0) 
{ 
// Otherwise calculate its distance and 
// mark it as visited 
qentry a = new qentry(); 
a.dist = (qe.dist + 1); 
visited[j] = 1; 
// Check if there a snake or ladder at 'j' 
// then tail of snake or top of ladder 
// become the adjacent of 'i' 
if (move[j] != -1) 
a.v = move[j]; 
else
a.v = j; 
q.add(a); 
} 
} 
} 
// We reach here when 'qe' has last vertex 
// return the distance of vertex in 'qe' 
return qe.dist; 
} 
public static void main(String[] args) 
{ 
// Let us construct the board given in above diagram 
int N = 30; 
int moves[] = new int[N]; 
for (int i = 0; i < N; i++) 
moves[i] = -1; 
// Ladders 
moves[2] = 21; 
moves[4] = 7; 
moves[10] = 25; 
moves[19] = 28; 
// Snakes 
moves[26] = 0; 
moves[20] = 8; 
moves[16] = 3; 
moves[18] = 6; 
System.out.println("Min Dice throws required is " + 
getMinDiceThrows(moves, N)); 
} 
}

Metin2 para kasma yolları için bu yazımızı okuyabilirsiniz.