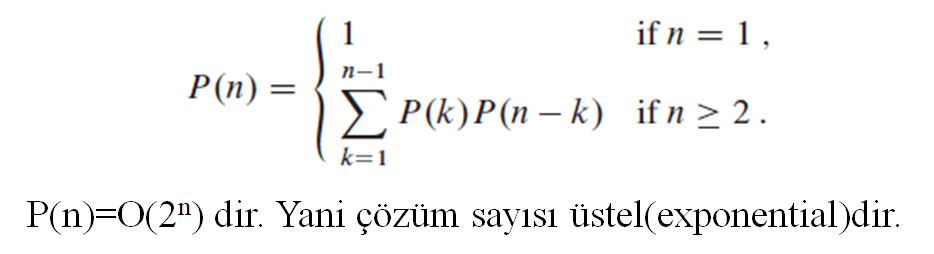Dinamik Programlama Nedir ve Nerede Kullanılır?

Bilgisayar bilimi, matematik, ekonomi ve biyoinformatikte dinamik programlama karmaşık bir problemi tekrarlanan alt problemlere bölerek, her bir alt problemi yalnız bir kere çözüp daha sonra bu çözümü kaydederek karmaşık problemin çözümünde kullanma yöntemidir.

Nerelerde Kullanılır?

Dinamik programlama, aynı çözümlü küçük problemlere parçalanabilen tüm problemler için uygulanabilir. Fakat brute-force ile exponential zamanda çözülebilen problemlerde gerçek değerini gösterir.

DP ile çözülebilecek birkaç problem:

• Rod-cutting problem
• Knapsack problem
• Matrix-chain multiplication
• Assembly Line Scheduling
• Birçok string problemi(LCS, longest increasing subsequence, Levenshtein distance)

Dinamik Programlama Algoritmasının Kurulması

Bir problem için dinamik programlama algoritması yapmak için aşağıdaki dört adım uygulanır.

1. Characterize the structure of an optimal solution (En iyi çözümün karakteristiğinin belirlenmesi)
2. Recursively define the value of an optimal solution(En iyi çözümün özyinelemeli tanımı)
3. Compute the value of an optimal solution,typically in bottom-up fashion(En iyi çözümün değerini top-down with memoization veya bottom-up yaklaşımdan birini kullanarak hesaplanması(genel olarak bottom-up))
4. Construct an optimal solution from computed information(Hesaplanmış verileri kullanarak en iyi çözümü bul)

Yazılan dört adımın ilk üç adımı dinamik programlamanın temel üç adımıdır. Eğer optimal çözümün yalnızca değerine ihtiyacımız varsa(Ör: LCS probleminde eşleşen harf sayısı) yalnızca ilk üç adımı kullanmak yeterli olacaktır.

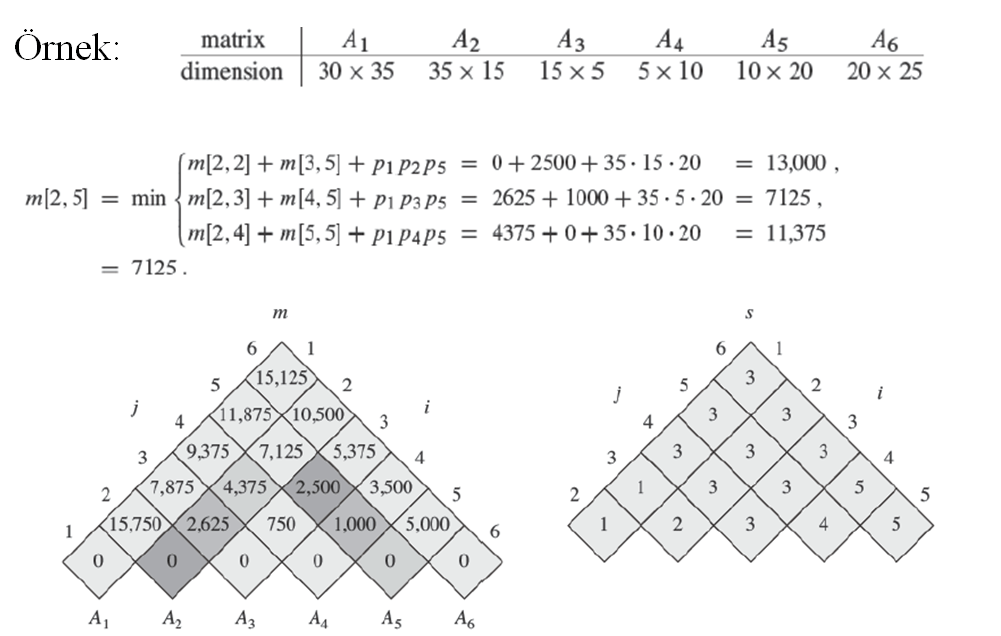
Zincir Matris Çarpımı

<A1,A2,…,An> matris zinciri olsun. C=A1A2…An çarpımı hesaplanmak isteniyor. Matris çarpımının birleşme özelliği vardır.

Bundan dolayı her türlü paranteze alma her zaman için aynı sonucu verecektir.

Örneğin <A1,A2,A3,A4> için beş tane farklı hesaplama yöntemi vardır.

• Seçilen yolun maliyet üzerindeki etkisini daha rahat görebilmek için <A1,A2,A3> zinciri ele alınsın.
• Boyutlar sırasıyla 10×100, 100×5, 5×50 olsun.
• p×q ve q×r boyutlarındaki iki matrisin çarpımında pqr tane skaler çarpım işlemi gerçekleştirilir.

1. Alternatif:

  Bu üç matrisin çarpımı ((A1A2)A3) parantezlemesine göre yapılırsa, A1A2 matrislerinin çarpımında 10.100.5=500 tane skaler çarpım yapılır.

  Elde edilen sonuç matrisin boyutları 10×5 olur.

  Bu matris ile A3 matrisinin çarpımı içinde 10.5.50=2500 tane skaler çarpım yapılır.

  Toplam olarak 7500 tane skaler çarpım yapılır.

2. Alternatif:

Eğer matrisler (A1(A2A3)) şeklinde çarpılırlarsa, A2A3 matrislerinin çarpımı için 100.5.50=25000 tane skaler çarpıma ihtiyaç vardır.

  Elde edilen sonuç matrisinin boyutları 100×50 olur.

  Bu matris ile A1 matrisinin çarpımı için de 10.100.50=50000 tane skaler çarpımyapılır.

  Toplam olarak 75000 tane skaler çarpım yapılır.

DP: Zincir Matris Çarpımı

Çarpılacak olan n tane matris için yapılabilecek parantez sayısı P(n) olsun. Bu durumda P(1)=P(2)=1 olur ve P(3)=2, P(4)=5 olur. Fakat n büyüdüğü zaman yapılabilecek parantez sayısı da oldukça hızlı artacaktır.

Aşağıdaki yineleme bağıntısı n boyutlu matris zinciri için farklı parantezleme sayısını verir.

  Zincir Matris Çarpımı (Dinamik Programlama ile Çözümü)