Warshall Algoritması Nedir? Ne İşe Yarar?

Warshall Algoritması Nedir?
Bilgisayar bilimlerinde, Warshall algoritması, pozitif veya negatif kenar ağırlıklarına sahip ağırlıklı bir grafikte en kısa yolları bulmak için bir algoritmadır. Warshall algoritmasının tek bir uygulaması tüm köşe çiftleri arasındaki en kısa yolların uzunluğunu bulacaktır.
Bilgisayar bilimlerinin önemli konularından olan algoritma analizi sırasında sıkça bahsi geçen bir algoritmadır. Algoritmanın ana amacı belirli bir graf üzerinde bir başlangıçtan(source) bir bitiş düğümüne (sink, end, target) en kısa yoldan (shortest path) ulaşmaktır.
Bu özelliğinden dolayı, maksimum akış (maximum flow) problemleri olarak bilinen, ve örneğin bir dağıtım şebekesinde bir kaynaktan bir hedefe gönderilebilecek azami miktarı sevk eden problemlerin çözümünde kullanılabilen bu algoritma, algoritmayı bulan iki kişinin ismi ile anılmaktadır.
Algoritma basitçe bir grafta gidilebilecek düğümlerin komşuluk listesini (adjecency list) çıkararak bu düğümlere olan mesafeyi tutan bir masfuf (matris) üzerinden çalışır.
Algoritmanın her adımında matris üzerinde çeşitli işlemler yapılarak en kısa yol bulunmaya çalışılır.
Algoritma matris üzerinde çalışan ve düğümler arası mesafeleri her adımda güncelleyen bir algoritma olduğu için itartif (iterative, döngü ile) yazılabilir.
Warshall Algoritmasının Kullanım Alanları
Floyd-Warshall algoritması aşağıdaki amaçlar için kullanılabilir:
- Yönlü graflarda en kısa yolun bulunması için. (Yukarıda bu durumu gösteren bir örnek bulunmakta)
- Bir düğümden seyahat edilebilecek diğer düğümlerin bulunmasında (transitive closure). Örneğin matrisin ilk halinde gidilemeyen düğümler sonsuz değerine sahiptir. Şayet matris işlendikten sonra hala sonsuz değerine sahip matris elemanı bulunursa bunun anlamı o satır ve sütündakı düğümler arasında gidişin aktarmalı da olsa mümkün olmadığıdır.
- Düzenli ifadelerde (regular expressions) herhangi bir tekrarlı olayın tespiti için kullanılabilir. Kleen yıldızı (kleen’s algorithm) şeklinde tekrar eden ifadelerin bulunmasına yarar. Şayet çıkan matriste bir düğümden diğer düğüme giden yol sonsuz değilse ve diyagona göre simetriği olan yol da sonsuz değilse bir kleen yıldızı üretilebilir.
- Ağ programlamasında özellikle yönlendirici algoritmalarında (routing algorithms) en kısa yolun tayin edilmesinde kullanılabilir.
- Yönsüz bir grafın (undirected graph), iki parçalı graf (bipartite graph) olup olmadığının bulunmasında kullanılabilir. Basitçe graftaki mesafelerin tamamını 1 uzunluğunda kabul edersek (veya mesafe olarak atlanan düğüm sayısını (hop count) kabul edersek) bu durumda bir düğümden gidilebilen bütün komşu düğümlerin mesafesi ya tek ya da çift olmalıdır. Bir düğümün hem tek hem de çift komşusu varsa bipartite değildir denilebilir.
Bu algoritmayı bir örnek üzerinde inceleyelim.
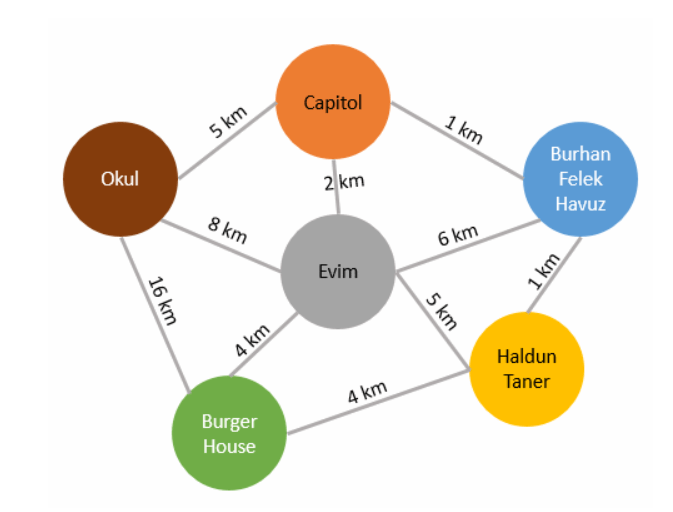
Biz evimizde oturuyoruz ve örneğin Haldun Taner sahnesine gideceğiz. Normal şartlarda direkt bir güzergah kullanırsak 5 km yol gitmemiz gerekiyor. Diğer yandan önce Capitol’e, oradan Burhan Felek’e ve oradan’da Haldun Taner’e geçersek toplamda 4 km yol katediyoruz. 1 km kazancımız var bu güzergahı takip edersek. Eğer önce Burhan Felek’e oradan Haldun Taner’e geçersek de 7 km yol kat edeceğiz. Senaryoyu biraz daha geliştirelim. Diyelim ki evden Burger House’a gideceğiz. Karnımız acıkmış. Doğrudan gidersek 4 km yol almamız lazım. Farklı güzergahlar da tercih edebiliriz. Örneğin Haldun Taner üzerinden geçersek 9km, Okul üzerinden geçersek 24km yol. Bunun gibi bir yerden diğer bir yere giderken pek çok güzergah ve mesafe belirlenebilir.
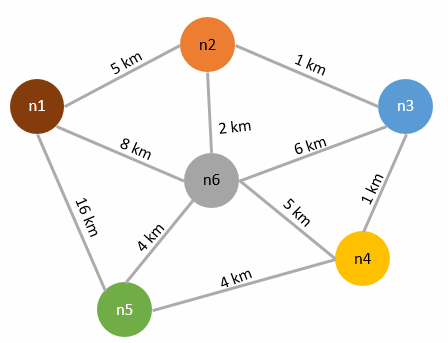
İşte Floyd-Warshall algoritması bir boğumdan diğer bir boğuma gitmek için kullanılabilecek en kısa yolların çıkartılmasında devreye girerek karar vermemizi kolaylaştırır. Şimdi yukarıdaki senaryoyu biraz daha bilimsel hale getirip lokasyonlar arasındaki en kısa mesafeleri bulmaya çalışalım. Öncelikle boğumlarımıza aşağıdaki gibi numaralar verelim ve ilk olarak yakınlık matrisimizi oluşturalım. (Yakınlık matrisinin ilk versiyonu boğumların komşu boğumlar ile arasındaki mesafelerini tanımlamaktadır)
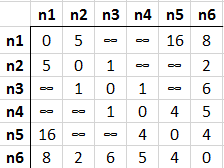
Bazı hücrelerde sonsuzluk sembolü, bazı hücrelerde ise sıfır değeri var. İki boyutlu bu matris boğumların en yakın diğer boğuma olan mesafelerini göstermekte. Bir boğumun kendisiyle arasındaki mesafe 0, doğrudan bağlı olmadığı bir boğumlar arasındaki mesafe ise sonsuz sembolü ile işaret edilmekte. Örneğin n1 boğumundan n3 ve n4 boğumlarına doğrudan bir hat olmadığı için sonsuz sembolü kullanıldı. Algoritmanın becerisi sonsuz sembollerini eritmek ve hatta sayısal değer alan hücrelerde olabilecek daha kısa mesafeler var ise bunları matris üzerinde güncellemektir.
Örneğin n1’den n3’e direkt gidişimiz olmadığından sonsuz olarak işaretlenmiş durumda. Oysa ki n1->n2->n3 şeklinde bir ulaşım var. Yani n2 üzerinden geçiş yaparak n3’e varabiliriz. Elbette n3’e varmak için n6 üzerinden de hareket edebiliriz. Yani n1->n6->n3 şeklinde bir güzergah da söz konusu olabilir. Hatta n1->n5->n4->n3 şeklinde de gidebiliriz.
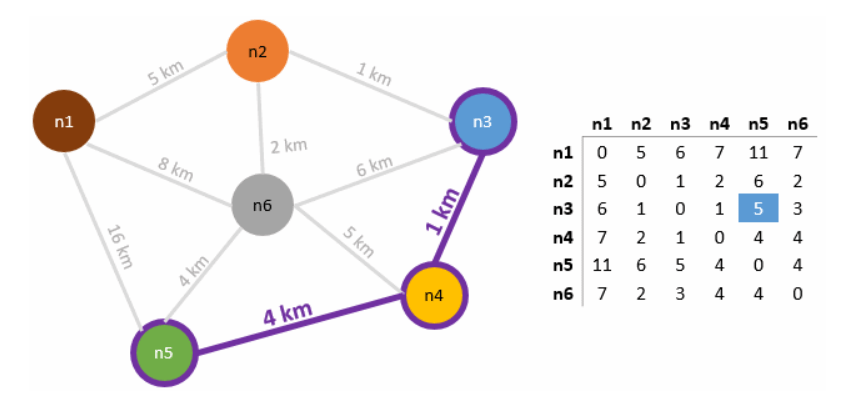
Buna göre bir noktadan bir noktaya gidilebilecek en kısa mesafeler bulunmuştur. Örneğin n3 noktasından n5 noktasına gitmek istediğimizde en kısa güzergah 5km uzunluğunda olup n3->n4->n5 rotası şeklindedir. Diğer alternatif yollara bakıldığında gerçekten de en kısa mesafenin bu olduğu açıkça görülebilir.
Bu algoritma yazımız da ilginizi çekebilir!